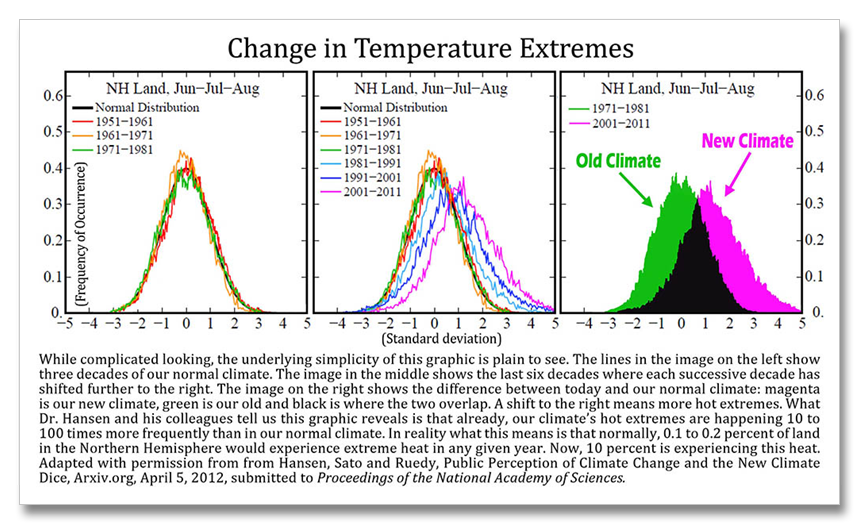
Across the northern hemisphere, extreme heat that once happened across 0.1 to 0.2 percent of the Northern Hemisphere now happens across ten percent–every year. The most extreme events are happening nearly 5,000 times more often than normal.
April 14, 2012: In Just the Last 30 Years, Climate Extremes Have Increased 10 to 100 Times— Dr. James Hansen could be the single most important climate scientists in the world. He has been the director of the NASA Goddard Institute for Space Studies (GISS) for30 years. He accused (successfully) the Bush Administration in 2005 of censoring climate science at GISS and retained his position as director. NASA GISS is the primary United States Government climate modeling agency. But Dr. Hansen’s creds are not the most important thing about Hansen, it’s his message. Today he has a paper “in” to the proceedings of the National Academy of Sciences of the Unties States of America that is unlike any before. The title is: “Public Perception of Climate Change and the New Climate Dice”. Hansen’s description of our new climate–the one we have already changed to, not the one that is predicted to happen in the future–is that the odds have changed as to whether or not we will see “normal” weather or “extreme” weather; hence the dice analogy. The concept is that the dice are now “loaded” to produce more sixes. Or more descriptively, more extreme weather. But most importantly(in my opinion), Hansen’s statistical work that evolved into this “dice analogy” is what is the real star of this paper. It can be seen in the Bell Curve analysis resulting form the statistical evaluation of the global temperature dataset and indeed, Hansen has created some “groovy graphics.”
Hidden behind this laid back title and dice analogy are a few ominous facts about how much our current climate has changed that I need to share before I get to the “groovy graphics.” Hansen his team tell us that “the odds of an unusually warm season have increased greatly over the past three decades” and, “A new category of hot summertime outliers . . . has emerged, with the occurrence of these outliers having increased 1-2 orders of magnitude [10 to 100 times] in the past three decades. Thus we can state with a high degree of confidence that extreme summers, such as those in Texas and Oklahoma in 2011 and Moscow in 2010, are a consequence of global warming, because global warming has dramatically increased their likelihood of occurrence.”
Not only is this one of the most forward leaning pieces of outreach ever written by such an authoritative individual, but it has a visual way of showing the increase in extremes in the last three decades. I new there was an excellent message in Hansen’s graphics but it took me a week to figure out how to present it. I am still in awe of how this graphic visualizes so well the changes that have already happened. It shows the amount of shift in our climate already and not what is predicted to happen in the future. One must understand statistics to be able to understand what this graph means, but a visual inspection shows what you need to know and I will try to explain the statistics the best I can. And btw, when I asked Dr. Hansen if I could modify his graph he said “of course”(!)
I’ve split apart a few key elements of this work to more readily show the message. Hansen’s original graphic is the one in the middle. On the left I have removed the curves for the decades 1981 to 2011. On the right I have colored in the curves under 1971-1981 (green) and 2001-2011 (purple). Black is where the two curves overlap.
The decades from 1951 to 1981 show a stable climate snapshot. Even though previous decades were different (not shown–they were colder), this period represents our climate that allowed significant evolution of our modern industrial society. The scale on the left represents the frequency of occurrence. The numbers at the bottom (0 to +/-5) represent standard deviations. Three standard deviations represent 99.7 percent of all the data, two is 95.5 percent, one is 68 percent. Looking at the curves for 1951 to 1981 on the left, the temperatures events (daily temps) at the top of the curve happen most often, or about 40 percent of the time (0.40) in this “normal” dataset. The three standard deviations shown represent what is considered to be a “normal” data set. And in a normal data set, 3 standard deviations representing 99.7 percent of all data points means that 3 days out of 1000 have temperatures that are above or below the other 997 days.
Ok, go back and read that again, maybe Google standard deviation and check out the “Math is Fun page” and standard deviation. Or just move on to the middle graph, it’s not that critical. When we compare the successive climates of the 80s, 90s and 00s to the period 1951 to 1981, we see a decisive shift to the right. This means that more of the time, warmer temperatures are happening. A lot more of the time. The decades of 2001 to 2011 saw two standard deviations of change relative to the climate of 1951 to 1981.
These new events are expanding towards greater temperature changes, so the climate we are experiencing today, or more accurately of the decade 2001 to 2011, contains temperatures that are more than a third warmer than anything compared to 1951 to 1981. It’s hard to put down in words, but easy to visualize with the graph on the right. that purple are under the purple curve for 2001 to 2011 represents a lot of heat. The area in black? This is the reason that scientists say they can not tell exactly if any given weather event is caused by climate change. The two climates overlap (our old one and our new one).
Now the finally: Looking at the curves for 1951 to 1981 look on the far right, where the curve comes back down to the baseline. Only 0.3 percent of all the temperature records in the decades 1951 to 1981, or only about thirty three days in this thirty year period were either above or below any of the other 10918 other days in those three decades. In other words, what happens at the very edge of the curve in a normal year, that extra rare event at the edge of the curve has a 1 in 370 chance of the daily temperature being warmer or colder than all the other days in that decade.
Now look at the big purple blob in the far right graph. The purple goes out to five standard deviations. Only three standard deviations are included in a “normal ” population of data. Anything other than that is considered statistically weird and generally not included in calculations or comparisons with the other data. But now our climate has changed. Five standard deviations represent 99.99994 percent of all events under “normal circumstances.”
What is happening today at the edge of the curve is two standard deviations beyond the normal edge of the curve. If we compare the edge of the curve today (2001 to 2011) to 1951 to 1981, that event at the edge of the five standard deviation curve has a 1 in 1,744,278 chance of happening. In other words, the most extreme events happening today are happening 4,714 times more often than “normal”!
Extra geeky explanation of science stuff: In case you caught the math discrepancy between 100 times more and 4,700 times more often: The paper says one to two orders of magnitude. This means add a zero to the numbers for one order of magnitude or add two zeros for two orders of magnitude. Referring to this as 10 to 100 times more is much more simple and close enough until more accurate numbers pop up that seem to discredit this simple explanation. One hundred times more that the 1 to 370 ratio of three standard deviations would be 1 to 370,000. for five standard deviations representing 1 to 1,744,278 times more we get a math equivalent of 471 times more. To reach three orders of magnitude it has to be 1,000 time more or greater. There are a number of things in this discussion (and many science discussions) that serve to create variable that move the target around so to speak. When this happens scientists refer to orders of magnitude in change. But because this is a nebulous term to most folks, I like to use more concrete descriptions and dispense with the details that tell us that the numbers I am referencing may be off by a hundred or more percent. The facts around these cases are that a few hundred percent is no big deal, it’s orders of magnitude that make a difference. But if one does not really understand the extra layer of complicate that arises form orders of magnitude the details causing the scientists to say orders of magnitude rather than more specific numbers, then it is much more of an impediment than if the details were understood. So I tend to use numbers that may be inaccurate, but the inaccuracy is not relevant to the greater discussion of detail–but all of this is opaque to the what I write, so why again am I telling you this? Oh, yes because I said 100 time greater in one spot and 4,700 times more frequent in another.
Hansen et al., Public Perception of Climate Change and the New Climate Dice, PNAS in publication.
http://arxiv.org/ftp/arxiv/papers/1204/1204.1286.pdf